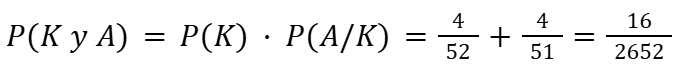Variables
LI: Los límites inferiores de clase son los datos más pequeños que pueden pertenecer a las diferentes clases.
LS: Los límites superiores son los datos más grandes que pueden pertenecer a las diferentes clases.
C: La amplitud de clase es la diferencia entre las fronteras superior e inferior.
K: El número de clases es el número de clases que debemos establecer en base a la cantidad de muestra.
M: La marca de clase es el valor medio del intervalo de clase.
F: Frecuencia de clase acumulada

Construcción de una distribución de frecuencias
1. Decidir el número de clases: 
2. Calcular amplitud de clase: 
3. Formar los intervalos de clase:

• Primer LI = Dato menor
• Siguiente LI = LI anterior + C
• LS = Siguiente LI - 1

4. Calcular la marca de clase y frecuencias: 

Medidas de tendencia central
1. Para datos no agrupados:
Media = 
Mediana = Dato del centro
Moda = Dato con mas frecuencia

2. Para datos agrupados
Media =
Mediana = 
Moda =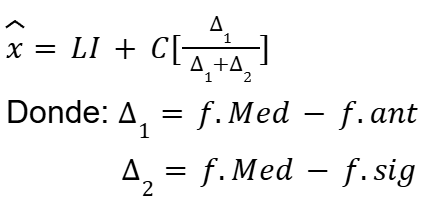 

Medidas de dispersión
1. Para datos no agrupados

Rango = Dato mayor - Dato menor
Desviación media =
Varianza =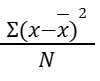
Desviación estándar =

2. Para datos agrupados
Varianza =
Desviación estándar = (Colocar notación)

Probabilidad de eventos compuestos
Eventos Mutuamente Excluyentes: la ocurrencia de uno imposibilita la ocurrencia del otro
Eventos Complementarios: el que no ocurra un evento garantiza la ocurrencia del otro
Eventos Independientes: el que ocurra uno de ellos no afecta la probabilidad de que se presente el otro

Fórmulas:
No ME: 
ME: 
Complementarios:
Independientes:
Dependientes:

Ejemplos:

1. Al sacar una carta de una baraja, ¿cuál es la probabilidad de sacar una figura (J, Q, K) o un diamante?
   
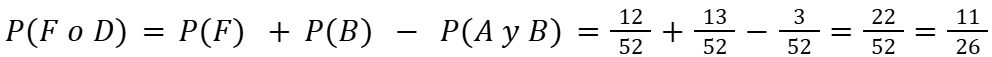
2. Una bolsa contiene 8 bolas verdes, 15 rojas y 7 negras. Si se extrae una, ¿cuál es la probabilidad de que sea verde o negra?
   
   
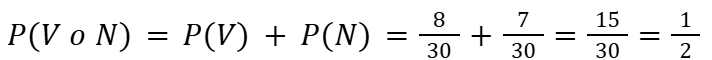
3. Calcule la probabilidad de que al lanzar un dado se obtenga 4 y de que al lanzar una moneda caiga águila.
   
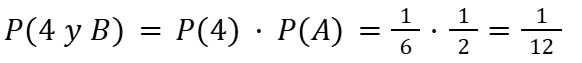
4. Calcule la probabilidad de sacar de una baraja un rey y luego un as.